Устный счёт в школе Сергея Рачинского
 Многие видели картину «Трудная задача». Другое название картины – «Устный счёт в сельской школе». Изображённое художником действительно происходит в сельской школе. Известно даже, что это за школа: школа села Татево Бельского уезда Смоленской губернии (теперь Татево относится к Оленинскому району Тверской области). Школа не обычная, а как сказали бы сегодня, авторская: школа Сергея Александровича Рачинского.  Художник Николай Петрович Богданов-Бельский, в 1895 году написавший эту картину, сам был выпускником Татевской школы. Именно С.А. Рачинский разглядел талант мальчика и устроил его учиться живописи сначала в иконописную мастерскую Троице-Сергиевой лавры, а потом в Московское училище живописи, ваяния и зодчества. Неудивительно, что благодарный ученик часто изображал своего учителя, а несколько наиболее известных картин Н.П. Богданова-Бельского посвящены родной школе.  На этом полотне Сергей Александрович внимательно слушает ответ, который мальчик, решивший пример раньше других, говорит ему шёпотом на ухо (чтобы другие не услышали). Но что за вычисление должны устно выполнить крестьянские дети? Задание написано на доске, и его вполне можно прочитать. 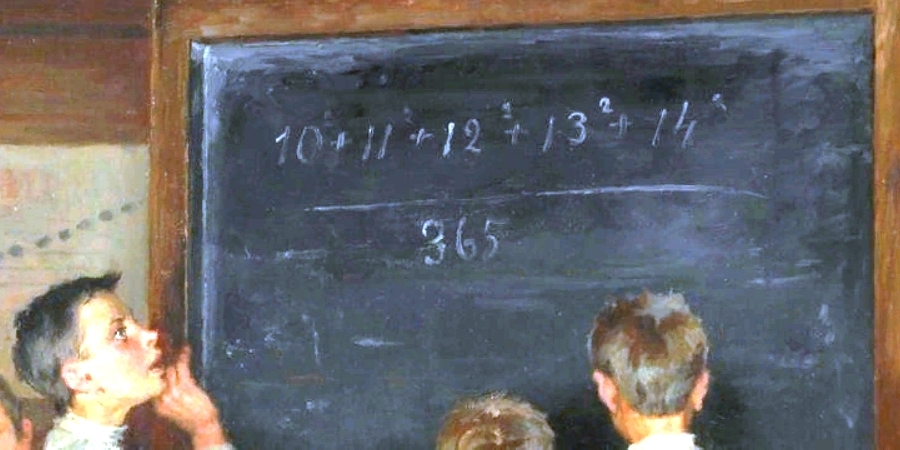 Запишем эту дробь одной строкой. (10²+11²+12²+13²+14²):365
Несколько степеней, сложение, а в конце ещё и деление на трёхзначное число! Как тут быть без калькулятора? Не сложновато ли для устного счёта? И всё же попробуем сосчитать. (10²+11²+12²+13²+14²):365 = (10²+11²+12²):365+(13²+14²):365
И вот здесь начинается самое интересное. 10²+11²+12²=100+121+144=365
13²+14²=169+196=365 (365+365):365=2 Ответ: 2.
Задание оказывается вполне посильным для устного счёта, при условии, что ученики наизусть знают квадраты двузначных чисел хотя бы до 14. А выполнив его, некоторые ещё и запомнят, чему равны суммы квадратов чисел 10, 11 и 12, а также 13 и 14 (365 дней в году - легко запомнить). Одно это уже даёт представление о серьёзном уровне подготовки, который давала деревенским детям школа Рачинского - начальная школа конца XIX века. Будущий художник Коля Богданов учился в ней приблизительно 140 лет назад! А что сейчас? Вот один из многих примеров, характеризующих математическую подготовку современных школьников: вопрос, заданный учеником на сайте подсказок. 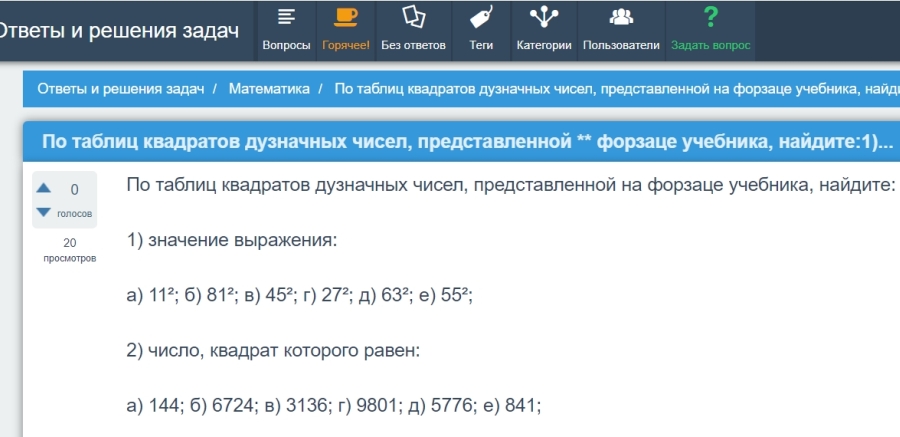 Сегодня ученики не то, что устно сосчитать – не могут даже сами посмотреть готовое решение в таблице квадратов целых натуральных чисел (она напечатана в учебнике, в задании даже указано, где именно), и спрашивают ответ в Интернете. Конечно, на это замечание можно возразить, что в наше время навыки устного счёта не столь актуальны, как полтора века назад. Теперь для вычислений у всех есть калькуляторы, смартфоны. Однако устный счёт не только вырабатывал вычислительные навыки. Он приучал действовать точно и последовательно, держать в памяти промежуточные результаты, концентрироваться на задаче и напрягать свой разум для её решения. Этих умений не хватает нынешним школьникам. Для ссылки: Сидоров С.В. Устный счёт в школе Сергея Рачинского [Электронный ресурс] // Сидоров С.В. Сайт педагога-исследователя – URL: http://si-sv.com/publ/v_shkole_sergeja_rachinskogo/16-1-0-733 (дата обращения: 10.03.2026). | |
| Опубликовано 03.11.2021 | Просмотров: 7445 | |
